Examining Influence Requirements
Analysis by detail251 - July 21, 2017
One of the most important topics in Magic: The Gathering (MtG) is how to build your mana base. Much has been written about this topic from an MtG standpoint. While the skill is almost completely transferable to Eternal, there isn't anything quite as in depth about it available for Eternal. Perhaps the most important article on the subject in the MtG world is one written by Frank Karsten back in 2013, you can find it here.
I consider this article mandatory reading for anyone serious about being a deck builder in any Magic like card game. Notably, Frank goes in to great detail on his method for calculating the probabilities as well as providing code so you can reproduce the numbers yourself and apply it to new problems. You should read that article as I am not going to spend much time discussing the underlying math. Unlike Frank, I am not a PhD in game theory and mathematics so I will leave that part to him. Instead, I want to discuss this approach from the Eternal point of view and apply this methodology to some Eternal specific cards (namely the Champion cycle) as well as the unique Eternal mulligan rules.
To start, we need to modify the code provided to accommodate the Eternal mulligan system, as well as 75 card decks. In Eternal, a mulligan hand is guaranteed to have exactly 2, 3, or 4 power with an equal probability of each case. Additionally you are only allowed a single mulligan. You can find my, modified, version of the initial Java program here if you are interested.
Edit: You can use the tool on Eternal Warcry now: Mana Base Probability Calculator
As I mentioned, the first thing I want to analyze are the Champions since they put very obvious pressure on our influence. Champion of Cunning specifically is probably the most important champion to have active on curve as you often don't want to play it out without aegis to protect it. Let's examine TonyGeeeee's recent 2nd place entry to this week's (July 15th) ETS tournament.
In this list Tony is running a total of 34 power sources, of which 22 produce primal influence. This count includes seek power and the favors as power sources. This will technically throw the math off a bit, but since I am using the probability conditional on drawing enough power anyway, and Champion of Cunning is more expensive than the searchers, we can assume we had the power to cast the searchers on curve as well (this might not be true for cheaper cards mind you). So given 22/34 sources are valid, how likely is Tony to be able to run out a shields up champion on turn 5 exactly?
With 20 good sources: Prob=0.18054343226459257
With 21 good sources: Prob=0.21890938296914847
***With 22 good sources: Prob=0.2615350785536276***
With 23 good sources: Prob=0.3104551114694215
With 24 good sources: Prob=0.3611157075107946
With 25 good sources: Prob=0.41719838152706323
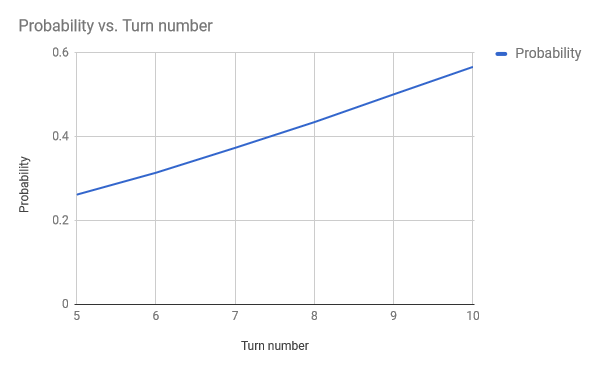
These are the probabilities that, assuming you have drawn 5 power sources, they all produce primal influence by turn 5. This means we are discounting games where we don't draw 5 power. About 26% from the looks of it. How about as the game progresses?
So we are looking at 50% by about turn 9, which would be a more typical play pattern than jamming the champion on turn 5. That isn't bad but it's not great. If we look at the initial numbers, it looks like we can get substantial improvement (10%) by adding just 2 more sources. That's as simple as swapping the 4th Vara's Favor for a 3rd Eilyn's Favor and a single Shadow Sigil for another Primal Sigil (or perhaps a Diplomatic Seal even though that isn't a straight 1 for 1 trade). Furthermore, doing this would give us nearly a 50% shot by as early as turn 7. We should consider the ramifications of this though. How would these changes (-2 Shadow for +2 Primal) affect our chances of playing Steward of the Past on turn 4 or Vara, Fate-Touched on turn 8? With these changes we would be running 21 Shadow sources of 34 total.
Probability of 2 sources on turn 4:
With 18 good sources: Prob=0.77262
With 19 good sources: Prob=0.8051
With 20 good sources: Prob=0.834876
***With 21 good sources: Prob=0.860465***
With 22 good sources: Prob=0.883687
With 23 good sources: Prob=0.90359
Probability of 3 sources on turn 8:
With 18 good sources: Prob=0.7292180805956565
With 19 good sources: Prob=0.7701830793210077
With 20 good sources: Prob=0.8081784677250416
***With 21 good sources: Prob=0.8417867750022303***
With 22 good sources: Prob=0.8706882984748473
With 23 good sources: Prob=0.8963030678462528
As you can see, even with these changes we are still ~85% to have Steward or Vara on curve (for comparison, prior to change we can see the numbers were both ~90%). Based on those numbers I would be inclined to recommend these changes. Making champion that much more reliably is totally worth a mere 5% drop for our premier Shadow requiring cards.
Next, I am going to examine how much more difficult each successively more expensive champion is to activate. Technically we should compare a list with identical power and influence counts, but I think it is more useful to compare based on a typical example of a deck you would actually find these champions in rather than in a vacuum. Intuition tells me that it is going to be far harder to have Champion of Cunning online turn 5 than a Champion of Glory by turn 2. What about having BOTH modes of glory active compared to only 1 mode of cunning? Modern Rakano Plate lists are running about 26 power with a 15/15 split on sources plus 4 Diplomatic Seals. In this case seal will count as either but not both. So I'll just add 2 to each influence count making it 17/17. This is guaranteed since by turn 2 is isn't possible to have more than 2 influence currently. This puts the odds of having a turn 2 glory with at least one mode active at 70%. This is not entirely accurate however, and the reason why becomes more clear when looking at the probability of having both modes active which is 24%. The issue is that some of the valid instances would have our second power coming in depleted since Rakano Banner won't necessarily have a 1 drop in play to power it up or you won't necessarily have a sigil in hand for Seat of Glory. Without wanting to complicate the math I would say we can expect a drop of several percent due to these conditions. Even then, it is interesting to note that glory will be fully active on turn 2 almost as often as cunning has a single mode active on turn 5 given a stock list. As one additional data point, Champion of Chaos is either 50 or 59% for the shadow and fire abilities respectively in a modern burn list (more on that in a minute). This is a prime example of why Champion of Progress and the new Champion of Mystery are so poor in comparison, each additional pip just further exacerbates the issue.
Let's have a look at a final example. Over the course of open beta Stonescar burn has been nerfed in a number of different ways. Most recently, many of the cards received influence increases. Most notably, Umbren Reaper and Soulfire Drake. These nerfs were sufficient to remove Umbren Reaper and Soulfire Drake from the majority of modern burn lists. Is this removal actually warranted though? How much more difficult to cast are Umbren Reaper and Soulfire Drake? Take TheSkeeJay's semi-finals deck from the same tournament:
Here, SkeeJay is running a total of 29 power sources, of which 15 are Shadow and 18 are Fire. I am going to ignore the Diplomatic Seals for the moment. This leads to the probability of success of:
With 13 good sources: Prob=0.32614272938201344
With 14 good sources: Prob=0.38116649254818297
***With 15 good sources: Prob=0.4363435350089861***
With 16 good sources: Prob=0.49107995492544354
With 17 good sources: Prob=0.5449288400823322
***With 18 good sources: Prob=0.5994661729570265***
43% for Umbren Reaper and 60% for Soulfire Drake. If we could squeeze a single extra Shadow source in this list (perhaps the 4th Vara's Favor in place of something) we could get Umbren Reaper up to just shy of 50%. At that point either card is likely playable, though clearly Soulfire Drake would be the better choice for this configuration. If we consider that we are about 15% to have a Diplomatic Seal in our opener which will increase the odds of hitting a few percent I think I'd be comfortable running Soulfire Drake in SkeeJay's list. How does this compare to previously? Here's an older style burn list from an ETS event back in March (pre-nerf):
This list is running 33 sources with a 22/20 F/S split. This gives:
With 18 good sources: Prob=0.827925
With 19 good sources: Prob=0.855712
***With 20 good sources: Prob=0.880702***
With 21 good sources: Prob=0.90286
***With 22 good sources: Prob=0.921017***
With 23 good sources: Prob=0.937367
With 24 good sources: Prob=0.950602
92 and 88% respectively for Soulfire Drake and Umbren Reaper. This is way higher than I was expecting. I would probably revise my initial conclusion based on this. I don't think even the 60% we could achieve for Soulfire Drake in the modern version of the list is acceptable. If I were going to play one of these cards in a modern list I would want to skew my list considerably more into one faction and try to get the probabilities to within 10% of pre-nerf. For a 29 source deck like SkeeJay's this means running 23 Fire or Shadow sources which would give 83%. I think the best way to go about this would be to remove all copies of Diplomatic Seal and replace them with just basic sigils. That would get you to where you need to be and since most early cards are only single faction requirement I don't think it would have TOO much of an adverse effect on your early game.
Going deep on the numbers here allow us to really see the limits of our influence base. Since that is what allows us to cast all our spells and units this is of critical importance. Beyond just knowing if a card will be castable it also can be used to tell if we aren't taking full advantage of what our deck can do. Steep influence requirements tend to come with a lot of raw power level so it would be a shame to leave some capability on the table for fear of overtaxing our power. These sorts of analyses aren't going to make a bad deck good, however, it will certainly tell you if you are doing something incredibly dumb, but that should be obvious already. What it will do, is take a good deck and make it slightly better than it was before. If that sort of edge doesn't appeal to you then you probably didn't make it this far in the article in the first place.
I consider this article mandatory reading for anyone serious about being a deck builder in any Magic like card game. Notably, Frank goes in to great detail on his method for calculating the probabilities as well as providing code so you can reproduce the numbers yourself and apply it to new problems. You should read that article as I am not going to spend much time discussing the underlying math. Unlike Frank, I am not a PhD in game theory and mathematics so I will leave that part to him. Instead, I want to discuss this approach from the Eternal point of view and apply this methodology to some Eternal specific cards (namely the Champion cycle) as well as the unique Eternal mulligan rules.
To start, we need to modify the code provided to accommodate the Eternal mulligan system, as well as 75 card decks. In Eternal, a mulligan hand is guaranteed to have exactly 2, 3, or 4 power with an equal probability of each case. Additionally you are only allowed a single mulligan. You can find my, modified, version of the initial Java program here if you are interested.
Edit: You can use the tool on Eternal Warcry now: Mana Base Probability Calculator
As I mentioned, the first thing I want to analyze are the Champions since they put very obvious pressure on our influence. Champion of Cunning specifically is probably the most important champion to have active on curve as you often don't want to play it out without aegis to protect it. Let's examine TonyGeeeee's recent 2nd place entry to this week's (July 15th) ETS tournament.
In this list Tony is running a total of 34 power sources, of which 22 produce primal influence. This count includes seek power and the favors as power sources. This will technically throw the math off a bit, but since I am using the probability conditional on drawing enough power anyway, and Champion of Cunning is more expensive than the searchers, we can assume we had the power to cast the searchers on curve as well (this might not be true for cheaper cards mind you). So given 22/34 sources are valid, how likely is Tony to be able to run out a shields up champion on turn 5 exactly?
With 20 good sources: Prob=0.18054343226459257
With 21 good sources: Prob=0.21890938296914847
***With 22 good sources: Prob=0.2615350785536276***
With 23 good sources: Prob=0.3104551114694215
With 24 good sources: Prob=0.3611157075107946
With 25 good sources: Prob=0.41719838152706323
These are the probabilities that, assuming you have drawn 5 power sources, they all produce primal influence by turn 5. This means we are discounting games where we don't draw 5 power. About 26% from the looks of it. How about as the game progresses?
So we are looking at 50% by about turn 9, which would be a more typical play pattern than jamming the champion on turn 5. That isn't bad but it's not great. If we look at the initial numbers, it looks like we can get substantial improvement (10%) by adding just 2 more sources. That's as simple as swapping the 4th Vara's Favor for a 3rd Eilyn's Favor and a single Shadow Sigil for another Primal Sigil (or perhaps a Diplomatic Seal even though that isn't a straight 1 for 1 trade). Furthermore, doing this would give us nearly a 50% shot by as early as turn 7. We should consider the ramifications of this though. How would these changes (-2 Shadow for +2 Primal) affect our chances of playing Steward of the Past on turn 4 or Vara, Fate-Touched on turn 8? With these changes we would be running 21 Shadow sources of 34 total.
Probability of 2 sources on turn 4:
With 18 good sources: Prob=0.77262
With 19 good sources: Prob=0.8051
With 20 good sources: Prob=0.834876
***With 21 good sources: Prob=0.860465***
With 22 good sources: Prob=0.883687
With 23 good sources: Prob=0.90359
Probability of 3 sources on turn 8:
With 18 good sources: Prob=0.7292180805956565
With 19 good sources: Prob=0.7701830793210077
With 20 good sources: Prob=0.8081784677250416
***With 21 good sources: Prob=0.8417867750022303***
With 22 good sources: Prob=0.8706882984748473
With 23 good sources: Prob=0.8963030678462528
As you can see, even with these changes we are still ~85% to have Steward or Vara on curve (for comparison, prior to change we can see the numbers were both ~90%). Based on those numbers I would be inclined to recommend these changes. Making champion that much more reliably is totally worth a mere 5% drop for our premier Shadow requiring cards.
Next, I am going to examine how much more difficult each successively more expensive champion is to activate. Technically we should compare a list with identical power and influence counts, but I think it is more useful to compare based on a typical example of a deck you would actually find these champions in rather than in a vacuum. Intuition tells me that it is going to be far harder to have Champion of Cunning online turn 5 than a Champion of Glory by turn 2. What about having BOTH modes of glory active compared to only 1 mode of cunning? Modern Rakano Plate lists are running about 26 power with a 15/15 split on sources plus 4 Diplomatic Seals. In this case seal will count as either but not both. So I'll just add 2 to each influence count making it 17/17. This is guaranteed since by turn 2 is isn't possible to have more than 2 influence currently. This puts the odds of having a turn 2 glory with at least one mode active at 70%. This is not entirely accurate however, and the reason why becomes more clear when looking at the probability of having both modes active which is 24%. The issue is that some of the valid instances would have our second power coming in depleted since Rakano Banner won't necessarily have a 1 drop in play to power it up or you won't necessarily have a sigil in hand for Seat of Glory. Without wanting to complicate the math I would say we can expect a drop of several percent due to these conditions. Even then, it is interesting to note that glory will be fully active on turn 2 almost as often as cunning has a single mode active on turn 5 given a stock list. As one additional data point, Champion of Chaos is either 50 or 59% for the shadow and fire abilities respectively in a modern burn list (more on that in a minute). This is a prime example of why Champion of Progress and the new Champion of Mystery are so poor in comparison, each additional pip just further exacerbates the issue.
Let's have a look at a final example. Over the course of open beta Stonescar burn has been nerfed in a number of different ways. Most recently, many of the cards received influence increases. Most notably, Umbren Reaper and Soulfire Drake. These nerfs were sufficient to remove Umbren Reaper and Soulfire Drake from the majority of modern burn lists. Is this removal actually warranted though? How much more difficult to cast are Umbren Reaper and Soulfire Drake? Take TheSkeeJay's semi-finals deck from the same tournament:
Here, SkeeJay is running a total of 29 power sources, of which 15 are Shadow and 18 are Fire. I am going to ignore the Diplomatic Seals for the moment. This leads to the probability of success of:
With 13 good sources: Prob=0.32614272938201344
With 14 good sources: Prob=0.38116649254818297
***With 15 good sources: Prob=0.4363435350089861***
With 16 good sources: Prob=0.49107995492544354
With 17 good sources: Prob=0.5449288400823322
***With 18 good sources: Prob=0.5994661729570265***
43% for Umbren Reaper and 60% for Soulfire Drake. If we could squeeze a single extra Shadow source in this list (perhaps the 4th Vara's Favor in place of something) we could get Umbren Reaper up to just shy of 50%. At that point either card is likely playable, though clearly Soulfire Drake would be the better choice for this configuration. If we consider that we are about 15% to have a Diplomatic Seal in our opener which will increase the odds of hitting a few percent I think I'd be comfortable running Soulfire Drake in SkeeJay's list. How does this compare to previously? Here's an older style burn list from an ETS event back in March (pre-nerf):
This list is running 33 sources with a 22/20 F/S split. This gives:
With 18 good sources: Prob=0.827925
With 19 good sources: Prob=0.855712
***With 20 good sources: Prob=0.880702***
With 21 good sources: Prob=0.90286
***With 22 good sources: Prob=0.921017***
With 23 good sources: Prob=0.937367
With 24 good sources: Prob=0.950602
92 and 88% respectively for Soulfire Drake and Umbren Reaper. This is way higher than I was expecting. I would probably revise my initial conclusion based on this. I don't think even the 60% we could achieve for Soulfire Drake in the modern version of the list is acceptable. If I were going to play one of these cards in a modern list I would want to skew my list considerably more into one faction and try to get the probabilities to within 10% of pre-nerf. For a 29 source deck like SkeeJay's this means running 23 Fire or Shadow sources which would give 83%. I think the best way to go about this would be to remove all copies of Diplomatic Seal and replace them with just basic sigils. That would get you to where you need to be and since most early cards are only single faction requirement I don't think it would have TOO much of an adverse effect on your early game.
Going deep on the numbers here allow us to really see the limits of our influence base. Since that is what allows us to cast all our spells and units this is of critical importance. Beyond just knowing if a card will be castable it also can be used to tell if we aren't taking full advantage of what our deck can do. Steep influence requirements tend to come with a lot of raw power level so it would be a shame to leave some capability on the table for fear of overtaxing our power. These sorts of analyses aren't going to make a bad deck good, however, it will certainly tell you if you are doing something incredibly dumb, but that should be obvious already. What it will do, is take a good deck and make it slightly better than it was before. If that sort of edge doesn't appeal to you then you probably didn't make it this far in the article in the first place.
detail251 detail251+4032
Comments
No comments currently.
Login to make a comment.